The equation of a circle

Math
OI
Publish Date:   2022-12-09
Update Date:   2023-01-08

The equation of a circle

采用 DeepL 翻译，目前的问题是中文的句子我是凑好宽度写的，但是英文没有。

可能会在将来的版本中解决这个问题。

Using DeepL to translate, the current problem is that the Chinese sentences I am putting together are written with good width, but the English is not. I will probably fix this problem in a future version.

I. Standard equation of a circle

In a plane right angle coordinate system, if the coordinates of the center and radius of a circle are determined, the circle is uniquely determined.

Then the standard equation of a circle with $(a,b)$ as the center and $r$ as the radius is $(x - a)^2 + (y - b)^2 = r^2 ~(r > 0)$

In particular, the unit circle is $x^2 + y^2 = r^2$.

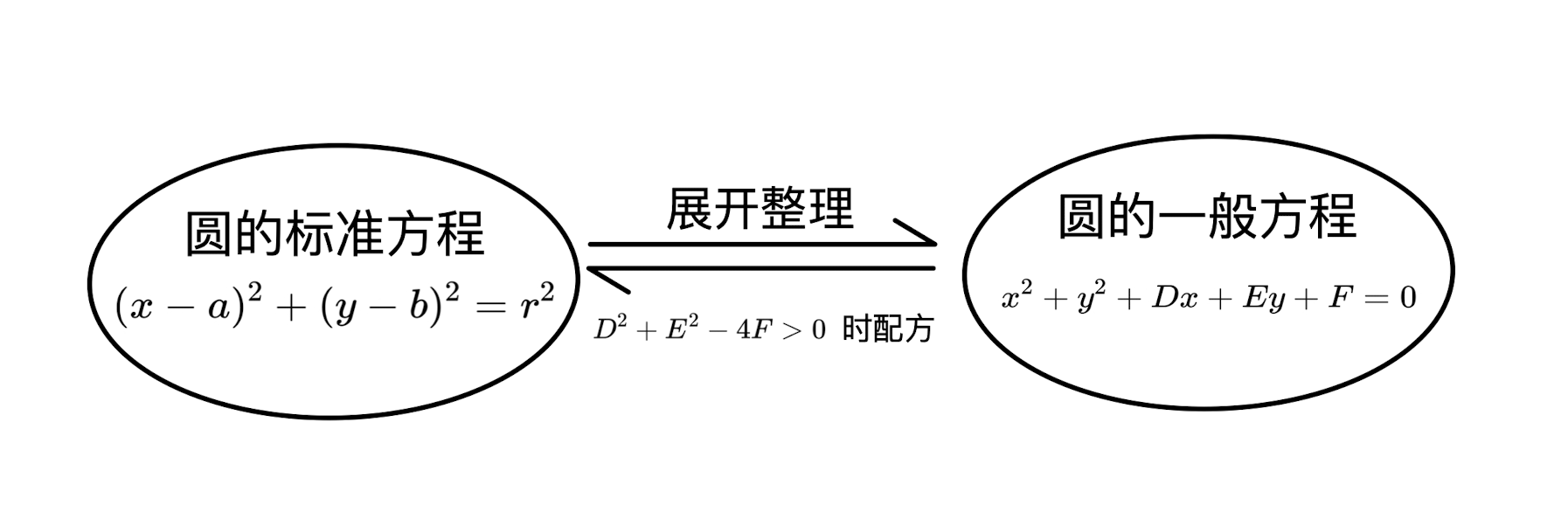
II. General equation of a circle

The equation $x^2+y^2+D x+E y+F=0\left(D^2+E^2-4 F>0\right)$ is called the general equation of a circle.

Converted to the standard equation as

  • When $D^2+E^2-4 F>0$, $x^2+y^2+D x+E y+F=0$ represents a circle.

    At this point the center of the circle is $\left(-\frac{D}{2},-\frac{E}{2}\right)$ and the radius of the circle is $\frac{\sqrt{D^2+E^2-4 F}}{2}$.

  • When $D^2+E^2-4 F=0$, $x^2+y^2+D x+E y+F=0$ denotes a point $\left(-\frac{D}{2},-\frac{E}{2}\right)$.

  • When $D^2+E^2-4 F<0$, $x^2+y^2+D x+E y+F=0$ does not represent any graph.

From the form of the equation, we know that the general equation of a circle contains three letters

Therefore, under general conditions, the general equation of the circle can be solved by always three independent conditions.

The following cases are more applicable to the general equation of a circle.

  1. Find the coefficients $D,E,F$ by substituting the coordinates of three points on a circle into the general equation of the circle.

  2. The two points on the circle and the line where the center of the circle is located are known

    Consider substituting two points into the equation of a circle by substituting the center of the circle $\left(-\frac{D}{2},-\frac{E}{2}\right)$ into the equation of the line in which the center of the circle lies and finding the coefficients $D,E,F$ to be determined.

Expand.

The relationship between the quadratic equation and the equation of a circle.

The binary quadratic equation $A x^2+B x y+C y^2+D x+E y+F=0$ forms a circle under the condition that

III. Position relationship between points and circles

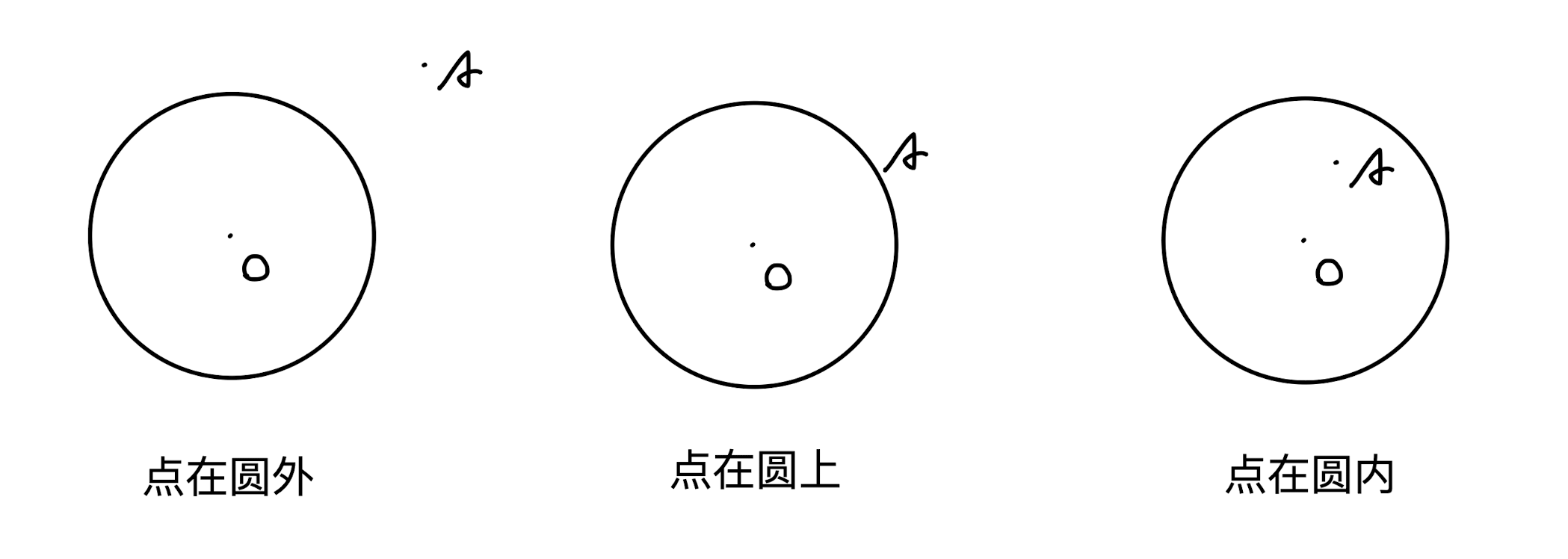
Judgment method.

  1. Geometric method: i.e., determine the relationship between $r$ and $|OA|$ in terms of magnitude.

  2. Algebraic method: Judging from the relationship between the coordinates of a point and the equation of a circle

    Standard equation: The point $P(x_0,y_0)$ is known and the equation of the circle $(x-a)^2+(y-b)^2=r^2$

    • The point $P$ is outside the circle, then $(x-a)^2+(y-b)^2 > r^2$.
    • The point $P$ is on the circle, then $(x-a)^2+(y-b)^2 = r^2$.

    • The point $P$ is inside the circle, then $(x-a)^2+(y-b)^2 < r^2$

      General equation: The point $P(x_0,y_0)$ is known and the equation of the circle $x^2+y^2+D x+E y+F=0$

    • The point $P$ is outside the circle, then $x^2+y^2+D x+E y+F > 0$.

    • The point $P$ is on the circle, then $x^2+y^2+D x+E y+F = 0$.
    • The point $P$ is inside the circle, then $x^2+y^2+D x+E y+F < 0$

Axial symmetry of a circle: the circle is symmetric about the line where the diameter is located.

The circle is symmetric about the point.

  1. To find a circle with known circle symmetry about a point, you only need to determine the location of the center of the circle you are looking for.

  2. If two circles are symmetric about a point, then this point is the midpoint of the line connecting the centers of the two circles.

  3. The circle is symmetric about the line

    1. To find a circle with known circle symmetry about a certain line, you only need to determine the position of the center of the circle you are looking for.

    2. If two circles are symmetric about a line, the line is the perpendicular bisector of the line joining the centers of the two circles.

V. Equation of trajectory and its solution

The equation of a trajectory refers to the equation of a curve formed by a moving point that moves according to certain rules.

There are three general methods to find the equation of the trajectory of a curve: the direct method, the substitution method, and the definition method.

1. direct method

The steps are as follows.

  1. Establish the right-angle coordinate system
  2. let $(x,y)$ denote the moving point $P$
  3. equate $x,y$ with the equation
  4. Simplify the equation. For some cases, special points on the curve may have to be discarded.

2. substitution method

Generally used to deal with an active point and a passive point

Simply find the relationship between the coordinates of these two points, and then substitute the equation of the trajectory satisfied by the active point to obtain the equation satisfied by the passive point.

3. definition method

Firstly, the known conditions and the definition of the curve to get what kind of curve for the trajectory, and then from the standard equation of this kind of curve to find the equation of the trajectory.

4. Example questions

Example.

If a point $P$ moves on a circle $C : x^2+y^2-8 x-6 y+21=0$ and $O$ is the origin, find the equation of the trajectory of the midpoint $M$ of the line $OP$.

Solution.

  1. Direct method (this question is solved in the same way as the substitution method).

    Let the coordinates of $M$ be $(x,y)$ and the coordinates of the point $P$ be $(x_0,y_0)$, then $x = \frac{x_0}{2}, y = \frac{y_0}{2}$, i.e. $x_0 = 2x,y_0 = 2y$.

    Since the point $P(x_0,y_0)$ is on the circle $C : x^2 + y ^ 2 - 8x - 6y + 21 = 0$

    So $x_0^2 + y_0^2 - 8x_0 - 6y_0 + 21 = 0$, so $(2 x)^2+(2 y)^2-8 \times(2 x)-6 \times(2 y)+21 = 0$.

    That is, the equation of the trajectory of the point $M$ is $x^2 + y^2 - 4x - 3y + \frac{21}{4} = 0$.

  2. Definition Method.

    As shown on the right, let the coordinates of the point $M$ be $(x,y)$ connected to $OC,PC$ and take the terminal $A$ of the line $OC$ and connect $MA$.

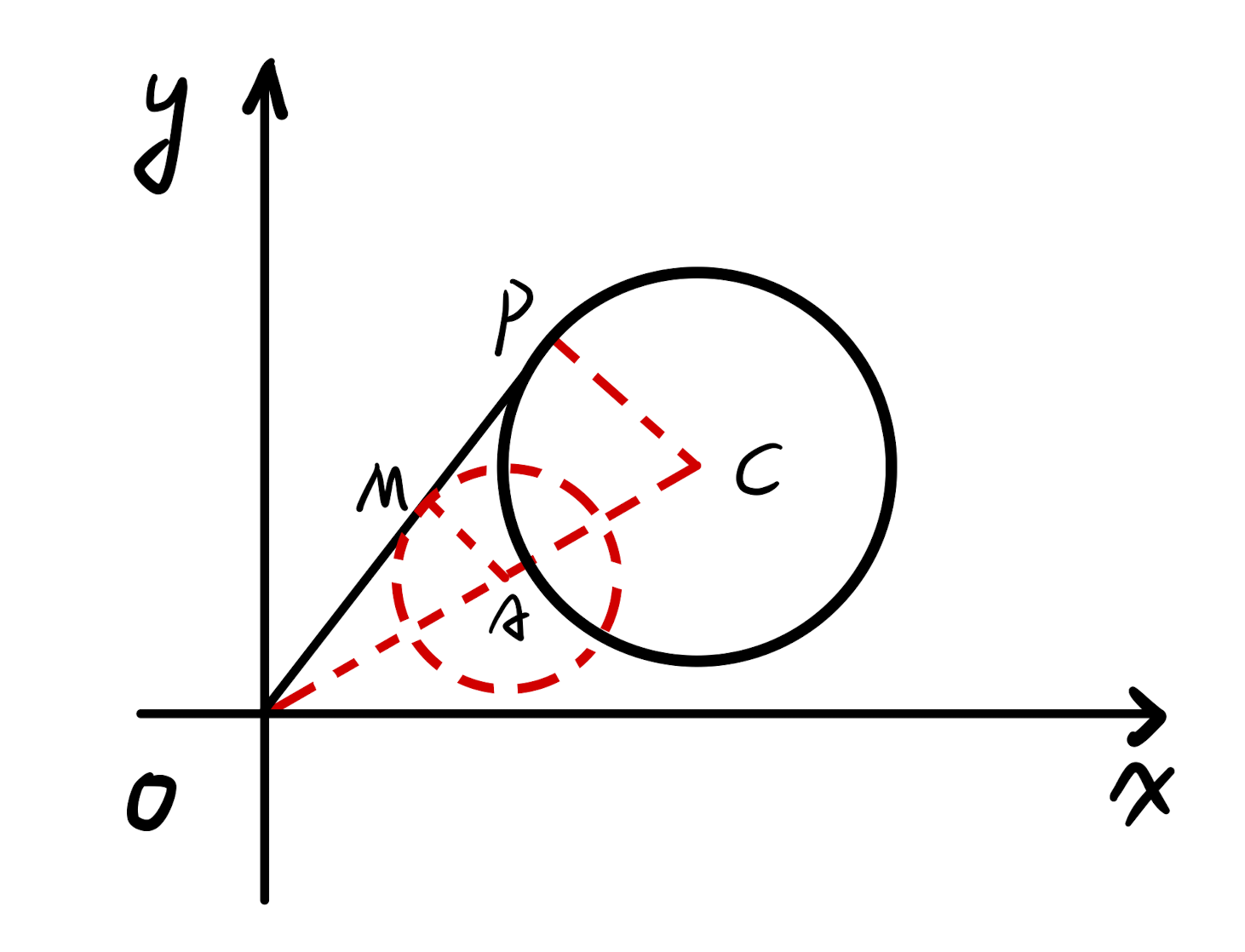
    The equation of the circle $C$ can be reduced to $(x - 4) ^ 2 + (y - 3)^2 = 4$ with the center $C$ at $(4,3)$ and $|CP| = 2$, then the coordinates of the point $A$ are $(2,\frac{3}{2})$.

    In $\triangle OCP$, $M,A$ are the midpoints of $OP,OC$, respectively, then $|M A|=\frac{1}{2}|C P|=1$

    When $O,C,P$ are co-linear, $|MA| = 1$, the path of $M$ is a circle with $A$ as the center and $1$ as the radius.

    Therefore, the equation of the trajectory of the point $M$ is $(x - 2)^2 + (y - \frac{3}{2})^2 = 1$.

VI. Maximum value of the distance from a point to a circle

Given a point $P(x_0,y_0)$ (not necessarily a fixed point), find the maximum and minimum values of $P$ to a point $Q$ on the circle $C:(x - a)^2 + (y - b)^2 = r^2$.

The answer is given here first.

Certificate.

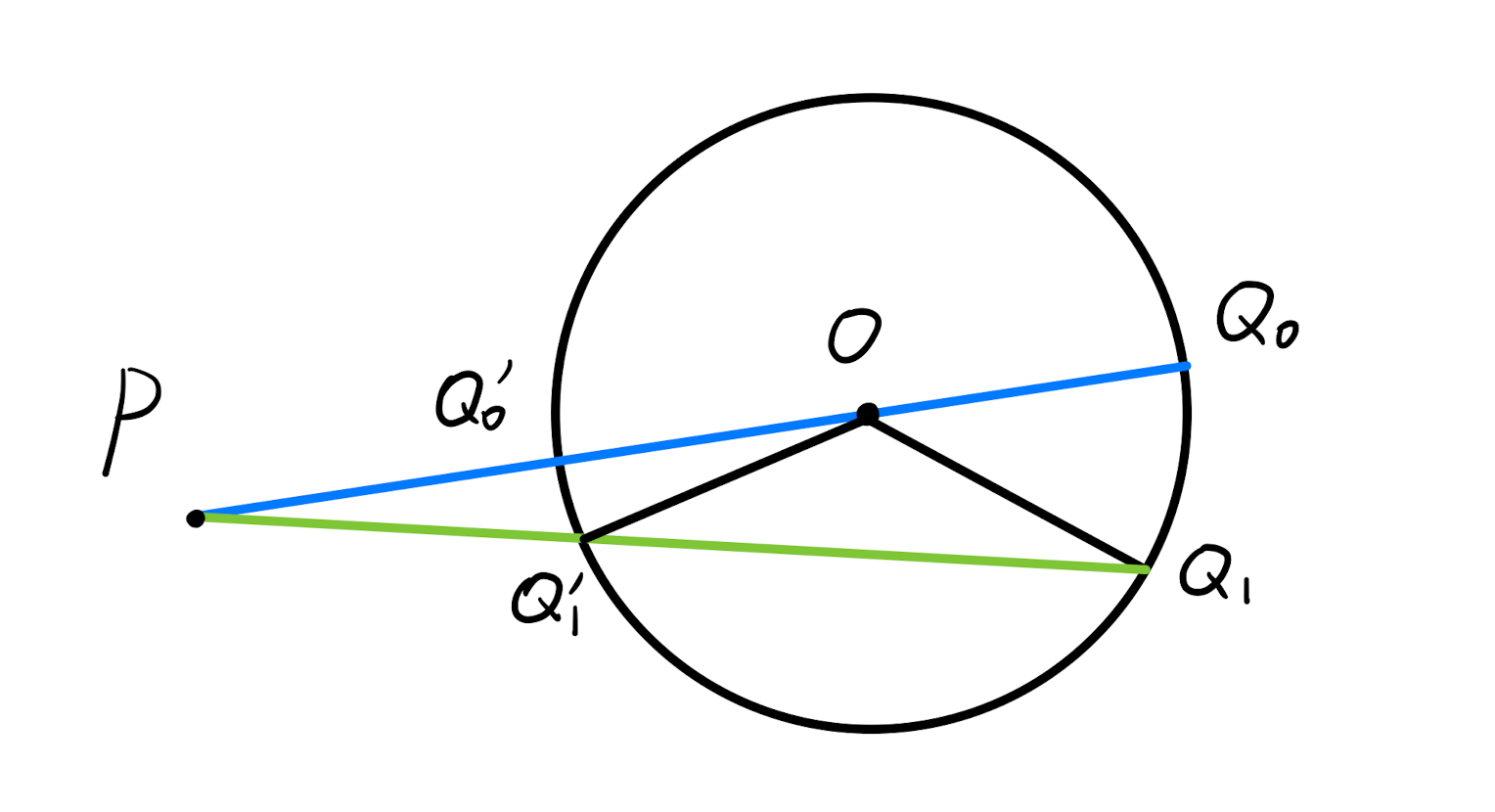
Consider the optimal $Q$ when the $P$ point is fixed, according to the conclusion $Q_0,Q_0^{\prime}$ which corresponds to the location of the $Q$ point when the maximum and minimum values are taken.

It is easy to find that $|PQ_0| = |PO| + |OQ_1| > |PQ_1|$, so the $Q$ point must be at $Q_0$ when taking the maximum value. $\square$

It is emphasized here that when fixing $P$, that is, $P$ is not necessarily a fixed point, but for each position of $P$, there exists a corresponding $Q_0$, and the conclusion still holds.

VII. Expansion: Apollonius Circle

1. definition reference

This is not in the scope of the entrance exam, but you can find out about it, and the exam will be given in the form of materials.

It is recommended to understand only the examples (~~ really someone like me idle to read the Chinese wiki ~~)

The Apollonios circles are two related families of circles. Each blue circle of the first circle family is orthogonal to each red circle of the second circle family. These circles form the base) of the bipolar coordinate system.

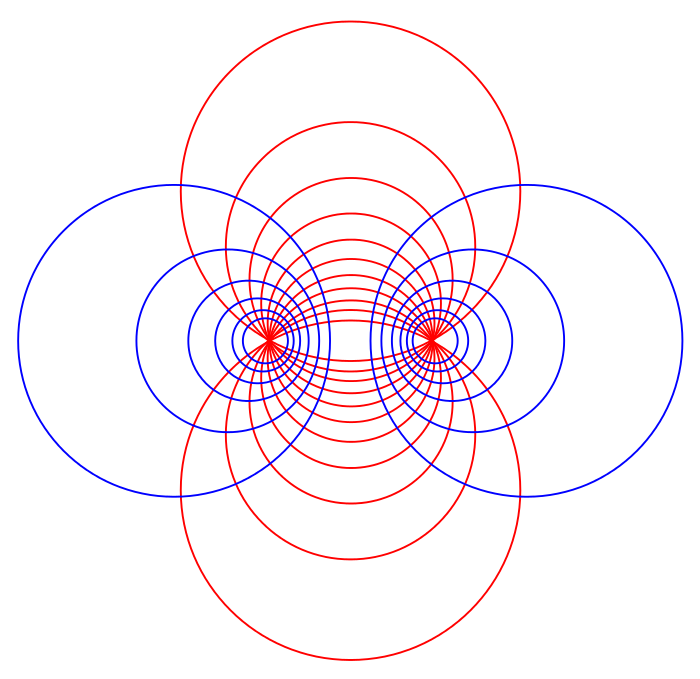
The Apollonios circle is defined by a line segment, label this line segment as $CD$.

First Family (Blue Circle)

Each circle in the first family is determined by a positive real number $r$, and these circles are defined as the trajectories of points $X$ that satisfy the following conditions

That is, the ratio of the distance from $X$ to $C$ to the distance from $X$ to $D$ is $r$.

When $r$ is very close to zero, the corresponding circle will be closer to the side of $C$ and vice versa to the side of $D$.

When $r=1$, the circle degenerates to the midline of the line $CD$.

Family II (red circle)

Each circle in the second family is determined by the angle $\vartheta$, and these circles are defined as the trajectories of points $X$ that satisfy the following conditions

where $\measuredangle CXD$ denotes the directed angle of CXD. When $\vartheta$ takes all values between $0$ and $\pi$, the above equation generates all circles passing through $C$ and $D$

2. Example questions

Apollonius was a famous mathematician in ancient Greece, who was called the three giants of mathematics in the Alexandrian period together with Euclid and Archimedes. He had a profound and systematic study of the circular pheasant curve, and his main research results were concentrated in his masterpiece “Theory of the Circular Pheasant Curve”.

The Apollonius circle is one of his research results and refers to.

We know that the ratio of the distance between the moving point $M$ and the two fixed points $A, B$ is $\lambda(\lambda>0, \lambda \neq 1)$, then the trajectory of the point $M$ is an Apollonius circle.

The Apollonius circle is $x^2+y^2=9$ if the ratio of the distance between the moving point $M$ and the two fixed points $A\left(\frac{9}{5}, 0\right), B(5,0)$ is $\frac{3}{5}$.

In the following, we examine a related issue.

Given a moving point $M$ on the circle $O: x^2+y^2=1$ and fixed points $A\left(-\frac{1}{2}, 0\right), B(1,1)$, then the minimum of $2|M A|+|M B|$ is _________.

Solution.

As shown, take the point $K(-2,0)$ and connect $OM,MK$.

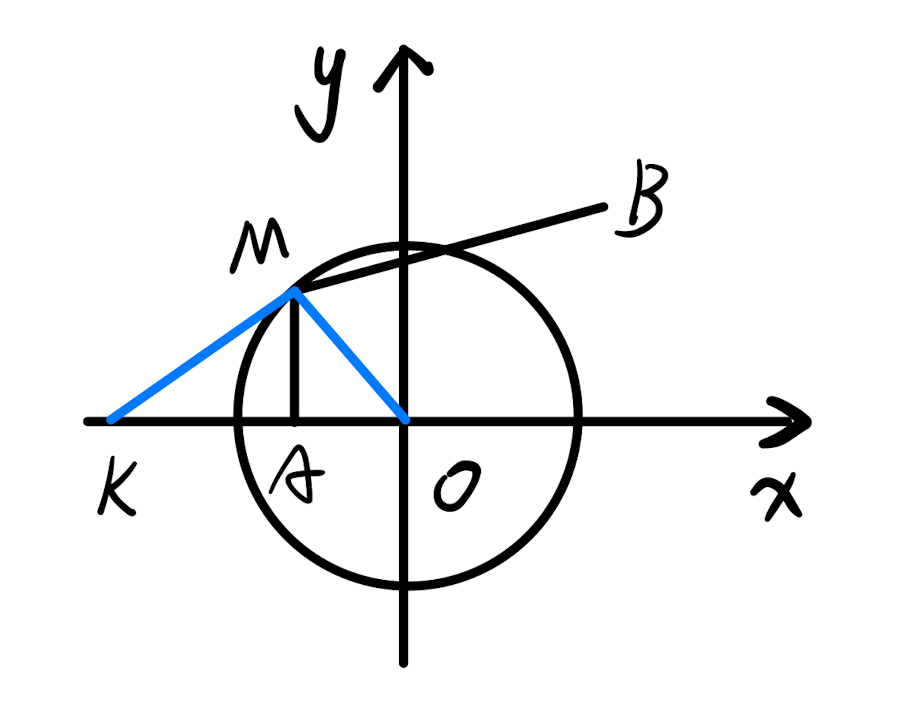
Since $|OM| = 1,|OA| = \frac{1}{2},|OK| = 2$, so $\frac{|OM|}{|OA|} = \frac{|OK|}{|OM|} = 2$.

And since $\measuredangle MOK= \measuredangle AOM$, so $\triangle MOK \sim \triangle AOM$, then $\frac{|M K|}{|M A|}=\frac{|O M|}{|O A|}=2$, so $|MK| = 2|MA|$.

So $|M B|+2|M A|=|M B|+|M K|$, and in $\triangle MBK$, $|MB| + |MK|\ge |BK|$, such that

Therefore, the answer is $\sqrt{10}$.

VIII. The position relationship between a line and a circle and determination

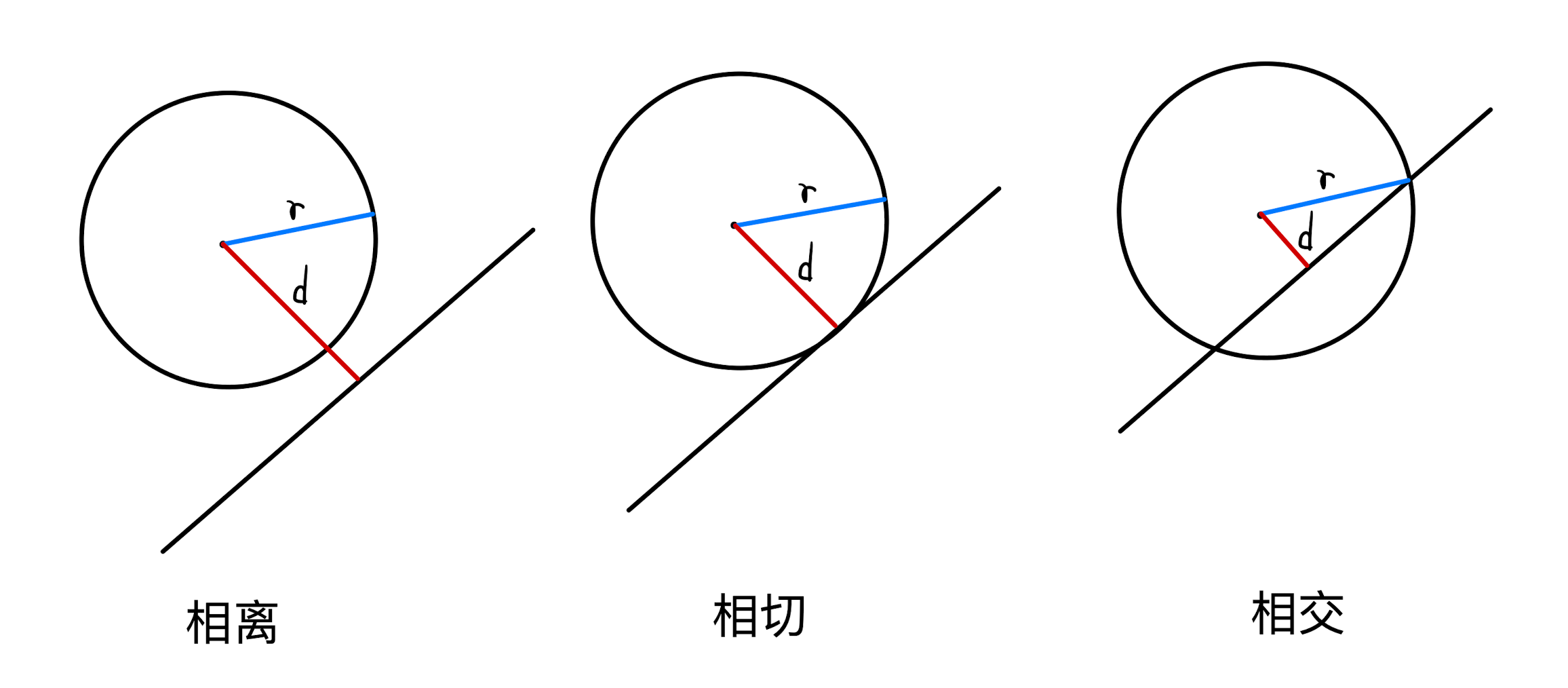
Judgment method.

  1. Algebraic method.

    A system of equations is formed by associating the equations of a line with those of a circle, and the system of equations is studied according to the number of solutions of the system of equations.

    • If $\Delta > 0$, the line intersects the circle.
    • If $\Delta = 0$ , then the line is tangent to the circle.
    • If $\Delta < 0$, the line is separated from the circle.

  2. Geometric method.

    Just determine the relationship between $d$ and $r$, as shown above ($d$ can be calculated using the point-to-linear distance formula)

IX. The tangent line problem of a circle and the method of solving the equation of the tangent line

Analysis of key ideas.

  1. When a line is tangent to a circle, the conclusion $d=r$ must be used
  2. When a line $l$ is tangent to a circle $C$, $l \ perp PC$.
  3. A tangent line from a point $P$ outside the circle to the circle $C$ with tangent point $Q$ must be used to $|PC|^2 = |PQ|^2 + r^2$.

A friendly reminder: there are many $(x_0,y_0)$ in the following, please do not confuse their meaning.

1. the number of tangent lines

The tangent line of a circle drawn through a point in the plane.

  • If the point is outside the circle, then two tangents to the circle can be made through this point.
  • If the point is on a circle, only one tangent line to the circle can be made through this point, and this point is a tangent line.
  • If a point is inside a circle, a tangent to the circle cannot be made through this point.

2. the equation of the tangent to the circle through a point outside the circle

The two tangents to the circle are drawn through a point outside the circle $P(x_0,y_0)$.

  1. First assume that the slope of the tangent line exists and is $k$ and that there are two ways to find $k$ as follows.

    1. Geometric method.

      Let the tangent equation $y - y_0 = k(x - x_0)$ , be reduced to the general equation $kx - y + y_0 - kx_0 = 0$.

      Since the line is tangent to the circle, the distance from the center of the circle to the line is equal to the radius, which leads to $k$.

    2. Algebraic method.

      Let the equation of the tangent line be $y - y_0 = k (x - x_0)$, in conjunction with the equation of the circle $(x - a) ^ 2 + (y - b) ^ 2 = r^2$

      The equation is reduced to a quadratic equation with respect to $x$, and then the discriminant is $0$ to find $k$.

  2. If only one slope $k$ is found by the above method, then the slope of the other tangent line must not exist, and the equation of the other tangent line is then $x = x_0$.

3. the equation of the tangent line with slope $k$ and tangent to a circle

  1. Geometric method.

    First, let the tangent equation be $y = kx + m$ and reduce it to the general equation $kx - y + m = 0$.

    Then use the distance from the center of the circle to the tangent line to equal the radius to find the equation $m$.

  2. Algebraic method.

    Let the equation of the tangent line be $y = kx + m$, and the equation of the circle $(x - a) ^ 2 + (y - b) ^ 2 = r^2$.

    The equation is reduced to a quadratic equation with respect to $x$, and then the discriminant is $0$ to find $m$.

4. the equation of the tangent line of a circle passing through a point on the circle

Set a point on the circle $Q(x_0,y_0)$ .

  1. Seeking method.

    First, find the slope of the line connecting the tangent point to the center of the circle $k(k \ne 0)$, then the slope of the tangent line is $-\frac{1}{k}$ by the vertical relationship

    The tangent equation can be obtained from the point-slope equation. If $k = 0$ or the slope does not exist, the tangent equation is obtained directly from the graph.

  2. Major findings.

    1. The equation of the tangent line across the unit circle $x^2 + y^2 = r^2$ is

    2. over the circle $(x - a)^2 + (y - b) ^ 2 = r ^ 2$, the equation of the tangent line is

    3. The equation of the tangent line across the circle $x^2 + y^2 + Dx + Ey + F = 0$ is

    Note that the tangent point chord equation that appears below has the same form as this equation, but the meaning of $(x_0,y_0)$ is different.

    Here $(x_0,y_0)$ refers to the coordinates of a tangent point on the circle, while the latter refers to the coordinates of a point outside the circle.

5. equation of the tangent chord of a circle and its solution

  1. Tangent chord Definition: Two tangents to a circle are drawn through a point outside the circle, and the line segment through the two tangent points is called the tangent chord of the circle.

  2. The equation of the tangent point chord is found.

    Directly finding the coordinates of the tangent point is extremely arithmetic, and considering set instead of .

    That is, set the coordinates of the tangent point, and then use the definition of the equation of the line to find the equation of the line where the two tangent points are located.

  3. Tangent Point Chord Equation: (You can use it directly for the big question, see Conic Curve - Tangent Point Chord Equation for the full version)

    The line $AB$ is the chord of the tangent point of the circle $C$ if $P(x_0,y_0)$ is drawn to two tangents $PA,PB$ of the circle $C$ from a point outside the circle.

    1. The equation of the tangent point chord across the unit circle $x^2 + y^2 = r^2$ is

    2. Over the circle $(x - a)^2 + (y - b) ^ 2 = r ^ 2$, the equation of the chord of the tangent point is

    3. The equation of the tangent point chord through the circle $x^2 + y^2 + Dx + Ey + F = 0$ is

    Note that the tangent point chord formula (in standard equation form) has the same form as the tangent point equation above, but $(x_0,y_0)$ means something different.

6. the method and formula for finding the length of the tangent to a circle

After talking so much about the equation equations, let’s look at the tangent length (

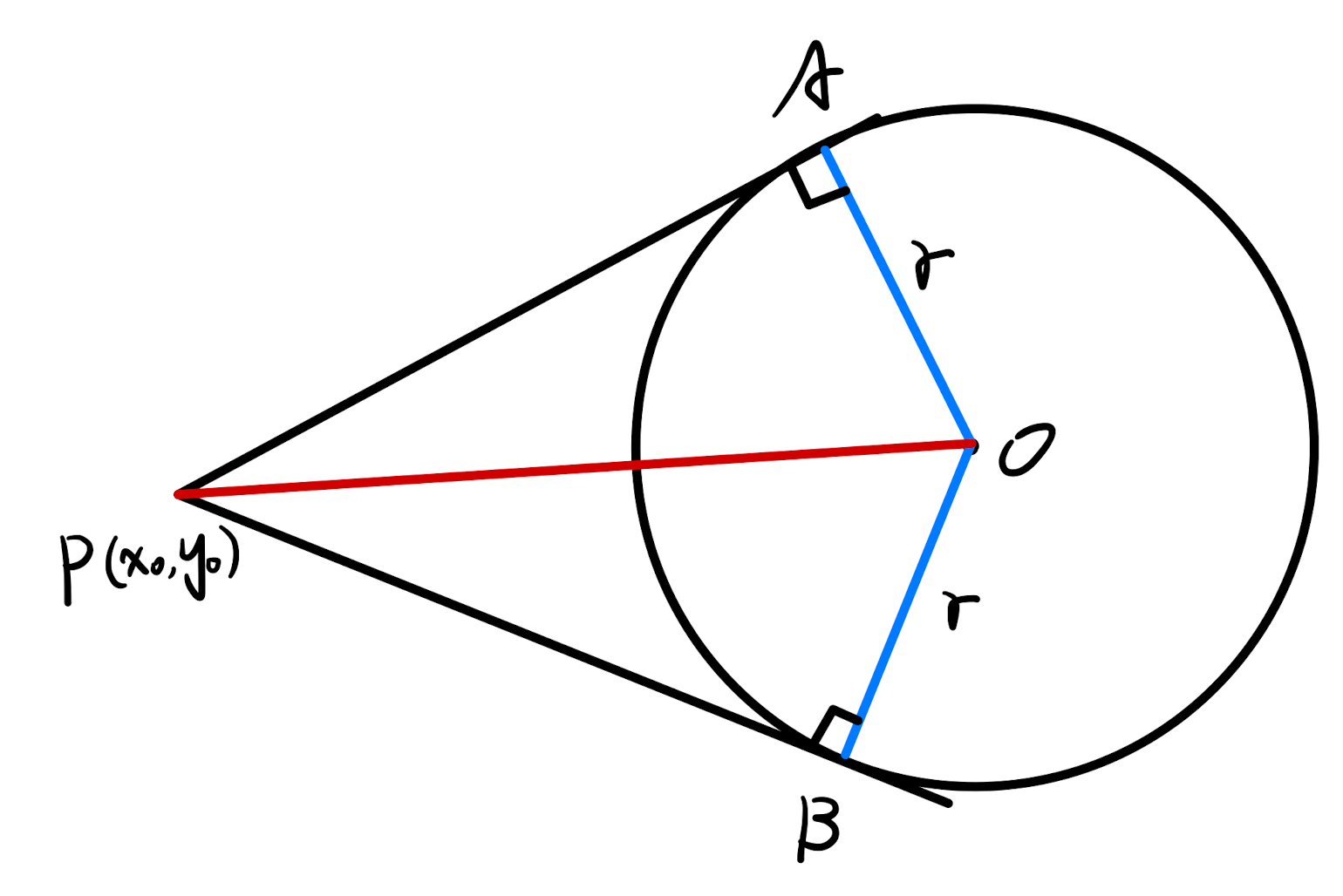
The two tangents to the circle are drawn through a point outside the circle $P(x_0,y_0)$.

  1. Geometric method: As shown below, in $\mathrm{Rt}\triangle AOP$ and $\mathrm{Rt}\triangle BOP$, the tangent length $|PA| = |PB| = \sqrt{|PO|^2 - r^2}$.

  1. Algebraic method.

    1. The length of the tangent line across the circle $(x - a)^2 + (y - b)^2 = r^2$ is

    2. The length of the tangent line across the circle $x^2 + y^2 + Dx + Ey + F$ is

X. Example of tangent line problem

Example 1.

Find the equation of the tangent line passing through the point $(1,-7)$ to the circle $x^2 + y^2 = 25$.

Solution: (three methods)

  1. It is easy to obtain that $(1,-7)$ is outside the circle and the line $x = 1$ is not a tangent.

    Let the slope of the tangent line be $k$ and the equation of the line is $y + 7 = k(x - 1)$ from the point-slope equation, i.e., $y = k(x-1)-7$.

    Substituting $x^2 + y^2 = 25$ by $\Delta = \left(2 k^2+14 k\right)^2-4\left(k^2+1\right)\left(k^2+14 k+24\right)=0$ yields $k = \frac{4}{3}$ or $k=-\frac{3}{4}$.

    The equation of the tangent line can be obtained by substituting $4x - 3y - 25 = 0$ or $3x+4y + 25 = 0$.

  2. It is easy to obtain that $(1,-7)$ is outside the circle and the line $x = 1$ is not tangent.

    Let the slope of the tangent line be $k$ and the equation of the line is $y + 7 = k(x - 1)$ from the point-slope equation, i.e., $kx-y-k-7 = 0$.

    From the tangent property of a circle, we know that the distance from the center of the circle $(0,0)$ to the line is $d = \frac{|0-0-k-7|}{\sqrt{1+k^2}} = r = 5$

    Then simplifying gives $12k^2 - 7k - 12 = 0$ and solving for $k = \frac{4}{3}$ or $k = -\frac{3}{4}$.

    The equation of the tangent line can be obtained by substituting $4x - 3y - 25 = 0$ or $3x+4y + 25 = 0$.

  3. The method is using the tangent point chord equation to find the tangent line equation.

    Let the equation of the tangent line be $x_0x + y_0y = 25$, where $(x_0,y_0)$ is the coordinate of the tangent point

    Substituting the coordinates of the point $(1,-7)$, we get $x_0 - 7y_0 = 25$

    From $\left\{\begin{array}{l}x_0-7 y_0=25 \\x_0^2+y_0^2=25\end{array}\right.$ we get $\left\{\begin{array}{l}x_0 = 4 \\\\ y_0 = -3\end{array}\right.$ or

    Therefore, the equation of the tangent line is $4x - 3y - 25 = 0$ or $3x+4y+25 = 0$.

Example 2.

The point $P$ is a moving point on the line $x+y-3=0$, and the tangent line from the point $P$ to the circle $O:x^2 + y^2 = 4$, the length of the tangent line is

Solution.

The tangent length $l = \sqrt{d^2 - r^2} = \sqrt{d^2 - 4}$, examining the value of $d$, it is easy to see that $d$ has only the minimum value.

Therefore $l \ge \sqrt{d_{\min}^2 - 4} = \frac{\sqrt{2}}{2}$ .

Example 3.

Make two tangents to the circle $C:x^2-4 x+y^2-4 y+5=0$ at the origin $O$. Let the tangents be $A,B$ and find the equation of the line $AB$.

Solution.

The formula is $-2x-2y+5 = 0$, and $-2x+2y-5=0$.

XI. The solution of the chord length problem of a circle

Let the equation of the line $l$ be $y = kx + m$ and the equation of the circle $C$ be $(x-a)^2 + (y-b)^2 = r^2$.

  1. Geometric method: It is easy to know from the figure below that $r^2 = d^2 + \left(\frac{l}{2}\right)^2$ .

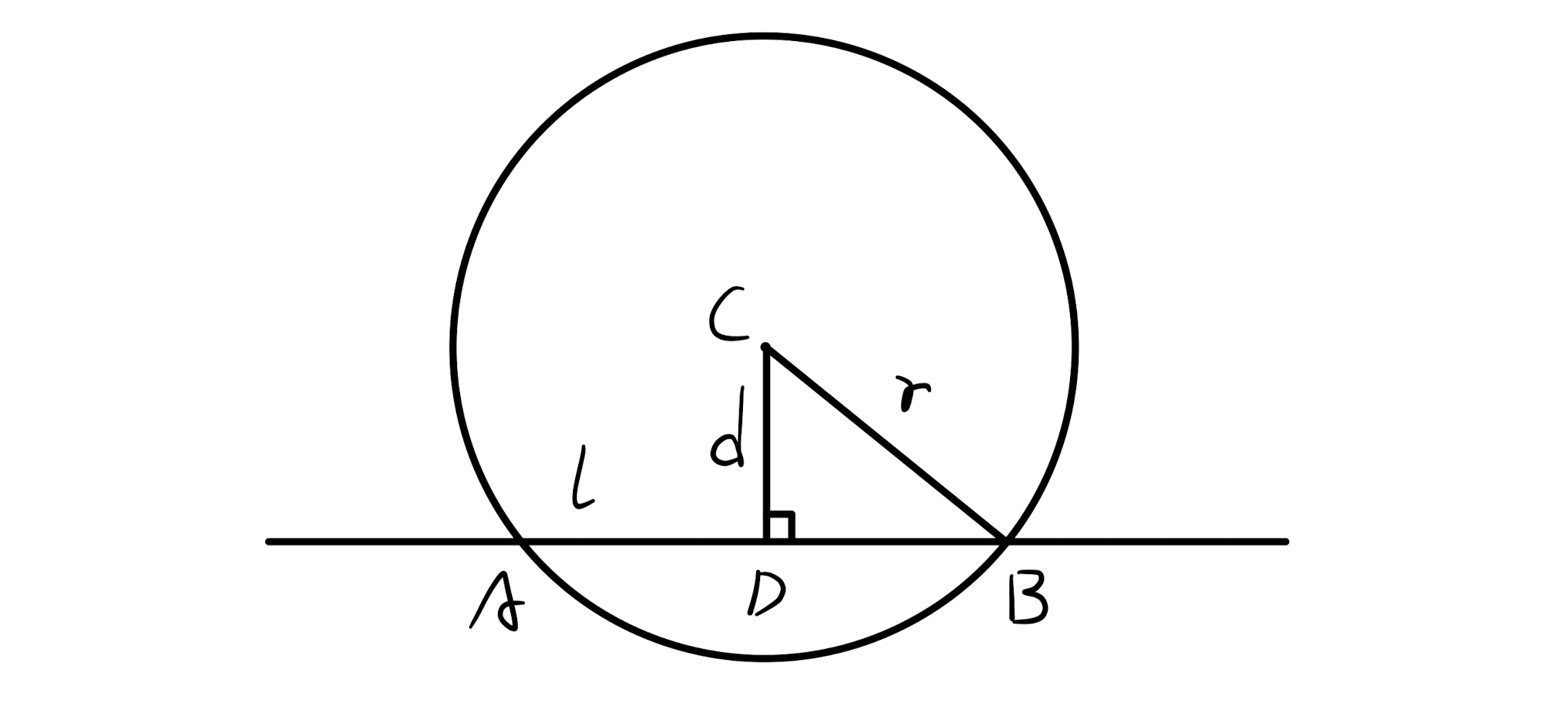
  2. Algebraic method.

    Form a system of equations between the equation of the line and the equation of the circle, and let the coordinates of the intersection points be $A(x_1,y_1), B(x_2,y_2)$ respectively.

    1. If the coordinates of the intersection point are simple to find, then the formula for the distance between two points is used directly to solve.

    2. If the coordinates of the intersection cannot be simply found, then the system of equations $\left\{\begin{array}{l}y = kx + m \\\ (x - a)^2 + (y - b) ^ 2 = r^2\end{array}\right.$ is eliminated to obtain a quadratic equation

      From the relationship between roots and coefficients in a quadratic equation, we have $x_1+x_2,~x_1x_2$ or $y_1 + y_2,~y_1y_2$, then we have

      $\tiny
      \begin{aligned}|A B| & =\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \[6pt]& =\sqrt{1+k^2}\left|x_1-x_2\right| \[6pt]& =\sqrt{\left(1+k^2\right)\left[\left(x_1+x_2\right)^2-4 x_1 x_2\right]}\end{aligned}$ or $\tiny\begin{aligned}|A B| & =\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \[6pt]& =\sqrt{1+\frac{1}{k^2}}\left|y_1-y_2\right| \[6pt]& =\textstyle\sqrt{\left(1+\frac{1}{k^2}\right)\left[\left(y_1+y_2\right)^2-4 y_1 y_2\right]}\end{aligned}$ （The formula here is not useful）

      The rectification gives $|A B|=\sqrt{1+k^2}\left|x_1-x_2\right|$ or $|A B|=\sqrt{1+\frac{1}{k^2}}\left|y_1-y_2\right|$ (the big question can be used directly)

Example 1.

The straight line $y=k x+3$ intersects the circle $(x-3)^2+(y-2)^2=4$ at the points $M, N$. If $|M N| \ge 2 \sqrt{3}$, find the range of values of $k$.

Solution.

The center of the circle $(x-3)^2+(y-2)^2=4$ is $(3,2)$ and the radius is $2$.

The distance $d = \sqrt{2^2-\left(\frac{|M N|}{2}\right)^2} \le 1$ from the center of the circle $(3,2)$ to the line $y = kx + 3$ from $|M N| \ge 2 \sqrt{3}$

The linear equation can be reduced to $kx - y + 3 = 0$, so $\frac{|3 k-2+3|}{\sqrt{k^2+1}} \le 1$ is solved by $-\frac{3}{4} \le k \le 0$, i.e. $k \in [-\frac{3}{4},0]$.

Example 2.

Let the line $y = x + 2a$ intersect the circle $C:x^2 + y^2 - 2ay - 2 = 0$ at the points $A,B$, and if $|AB| =2\sqrt{3}$, find the area of the circle $C$.

Solution.

The equation of the straight line can be reduced to $x - y + 2a = 0$ and the equation of the circle can be reduced to $(x-0)^2 + (y-a)^2 = \frac{4 a^2+8}{4}$.

Since $d = \frac{|0 - a + 2a|}{\sqrt{1^2 + 1^2}} = \frac{a}{\sqrt{2}}$, that is, $d^2 = \frac{a^2}{2}$, and $r^2 - d^2 = \left(\frac{l}{2}\right)^2$, substitute the solution to get $a^2 = 2$.

Therefore $r^2 = 4$, i.e. $S=\pi r^2 = 4 \pi$.

Example 3.

The straight line $y = kx - 1$ intersects the circle $C : (x + 3) ^ 2 + (y - 3) ^ 2 = 36$ at the points $A,B$. Find the range of values of the length of $AB$.

Solution.

Since the line $y=k x-1$ passes through the fixed point $(0,-1)$

So the maximum value of the distance from the center $(-3,3)$ of the circle $C$ to the line $y=k x-1$ is $\sqrt{[0-(-3)]^2+(-1-3)^2}=5$

The radius of the circle $C$ is $6$, and the minimum value of the length of $A B$ is $2 \sqrt{6^2-5^2}=2 \sqrt{11}$.

And when the line $y=$ $k x-1$ passes through the center of the circle the length of $A B$ takes the maximum value of the diameter $12$ , so $|A B| \in$ $[2 \sqrt{11}, 12]$ .

XII. Common methods for solving the most value problems associated with circles

1. use geometric properties to find the most value

To find the maximum and minimum values of a point on a circle to a line, you need to make a vertical line through the center of the circle to the line.

The longest chord passing through a point inside a circle is the diameter passing through this point, and the chord perpendicular to the longest chord passing through this point is the shortest chord.

In fact, there is nothing here, is the use of the chord length is also a bit to the distance of the straight line to deal with some problems.

2. solve the most value (range of values) problems using the position relationship between a line and a circle

The most value problem in an analytic set is generally based on the conditions to list the objective-function relationship

Then, according to the characteristics of the function relation, use the parametric method, the matching method, the discriminant method, etc., and apply the inequality to find its most value (range of values).

For the problem of the most value of a circle, the special geometric properties of the circle are used to solve the problem according to the geometric meaning of Eq.

  1. The most-valued problem of the form $u = \frac{y - b}{x - a}$ can be transformed into the most-valued problem of the slope of the moving line.
  2. The most-valued problem of the form $t = ax + by$ can be transformed into a most-valued problem with a moving linear intercept.
  3. The most-valued problem of the form $(x - a) ^ 2 + (y - b) ^ 2$ can be transformed into the most-valued problem of the square of the distance from the moving point to the fixed point.

Example 1.

The point $P(x, y)$ is known to be on the circle $C: x^2+y^2-6 x-6 y+14=0$.

  1. Find the maximum and minimum values of $\frac{y}{x}$.
  2. Find the maximum and minimum values of $x^2+y^2+2 x+3$.
  3. Find the maximum and minimum values of $x+y$.

Solution.

The equation $x^2+y^2-6 x-6 y+14=0$ can be reduced to $(x-3)^2+(y-$ $3)^2=4$.

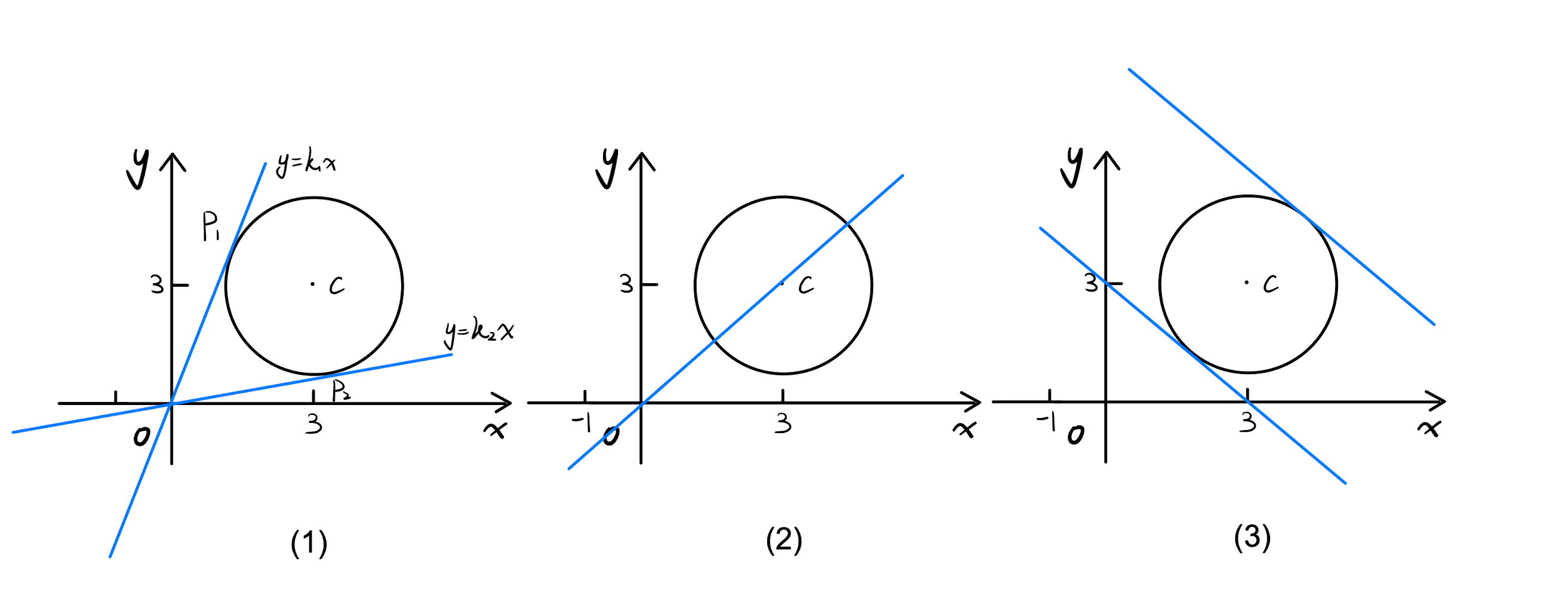
  1. $\frac{y}{x}$ denotes the slope of the line connecting the point $P$ on the circle to the origin, as in Figure 1 (below)

    Obviously $P O$ ($O$ is the origin) has the maximum or minimum slope when it is tangent to the circle.

    Let the equation of the tangent line be $y=k x$ (from the question, the slope must exist), that is, $k x-y=0$

    From the distance from the center of the circle $C(3,3)$ to the tangent line is equal to the radius, we can get $\frac{|3 k-3|}{\sqrt{k^2+1}}=2$ and solve for $k=\frac{9 \pm 2 \sqrt{14}}{5}$

    So the maximum value of $\frac{y}{x}$ is $\frac{9+2 \sqrt{14}}{5}$ and the minimum value is $\frac{9-2 \sqrt{14}}{5}$.

  2. $x^2+y^2+2 x+3=(x+1)^2+y^2+2$, which represents the square of the distance from the point $P$ on the circle to $E(-1,0)$ plus $2$

    Therefore, the equation is maximized or minimized when the distance between the point $P$ and the point $E$ is maximized or minimized.

    As in Figure 2, it is clear that the point $E$ is outside of the circle $C$.

    So the maximum value of the distance between the point $P$ and the point $E$ is $|C E|+2$ and the minimum value of the distance between the point $P$ and the point $E$ is $|C E|-2$.

    And $|C E|=\sqrt{(3+1)^2+3^2}=5$ ,

    So the maximum value of $x^2+y^2+2 x+3$ is $(5+2)^2+2=51$ and the minimum value is $(5-2)^2+2=11$.

  3. Let $x+y=b$, then $b$ denotes the intercept of the moving line $y=-x+b$ on the $y$-axis, as in Figure 3.

    Obviously when the moving line $y=-x+b$ is tangent to the circle $(x-3)^2+(y-3)^2=4$, $b$ obtains its maximum or minimum value.

    The distance from the center of the circle $C(3,3)$ to the tangent $x+y=0$ is equal to the radius of the circle

    Then $\frac{|3+3-b|}{\sqrt{1^2+1^2}}=2$, i.e. $|6 - b| = 2\sqrt{2}$, solving for $b = 6\pm 2\sqrt{2}$.

    Thus the maximum value of $x+y$ is $6+2 \sqrt{2}$ and the minimum value is $6-2 \sqrt{2}$.

XIII. The intersection of a line and a circle intersection problem

For problems involving the intersection of a line and a circle, the equations of the line and the circle can be combined to find the coordinates of the two points of intersection by solving the system of equations

However, when the corresponding system of equations is not easy to solve, the “set but not seek” strategy is often used to transform the whole, that is, first set the coordinates of the two intersection points, but not to find

Instead, the equation of a line is substituted for the equation of a circle, which is transformed into a quadratic equation by eliminating elements, and then the overall substitution is made using the relationship between roots and coefficients.

Common Steps.

  1. Set the coordinates of the two intersections $P\left(x_1, y_1\right), Q\left(x_2, y_2\right)$.
  2. use known conditions (e.g., two lines are perpendicular) to derive a relationship for $x_1, x_2, y_1, y_2$ (e.g., $x_1 x_2+y_1 y_2=0$)
  3. Combine the equation of the line with the equation of the curve, eliminating $y! ! $ (or eliminate $x! $) $! ! $ to get an equation for $x! ! $ (or on $y! $) $! ! $ quadratic equation that computes $\Delta$.
  4. Use Veda’s theorem to show $x_1+x_2, x_1x_2$ or $y_1+y_2, y_1y_2$.
  5. Substitute into the relation determined from step 2 and simplify
  6. verify that $\Delta>0$.

Example question.

Knowing the circle $C: x^2+y^2-2 x+4 y-4=0$, does there exist a line $l$ with slope $1$

What is the diameter of the circle whose diameter is the chord $A B$ of the circle $C$ intercepted by $l$ passing through the origin? If so, find the equation of the line $l$; if not, state the reason.

Solution.

Let there exist a line $l$ satisfying the problem and the equation $y=x+b$.

By $\left\{\begin{array}{l}y=x+b, \\\ x^2+y^2-2 x+4 y-4=0\end{array}\right.$ eliminating $y$, we have $2 x^2+2(b+1) x+b^2+4 b-4=0$.

Let $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ , then $x_1+x_2=-(b+1), x_1 \cdot x_2=\frac{b^2+4 b-4}{2}$

Since $y_1 \cdot y_2=\left(x_1+b\right)\left(x_2+b\right)=x_1 \cdot x_2+b\left(x_1+x_2\right)+b^2$, and the circle with $A B$ as its diameter passes through the origin

So $O A \perp O B$. Therefore, we have $k_{O A} \cdot k_{O B}=-1$, i.e. $x_1x_2+y_1y_2=0$

So we have $b^2+3 b-4=0$ and we have $b=1$ or $b=-4$.

Therefore, there exists a line $l: x-y+1=0$ or $x-y-4=0$ that satisfies the question.

XIV. The relationship between the position of the circle and the circle and the judgment method

1. Types of location relationships

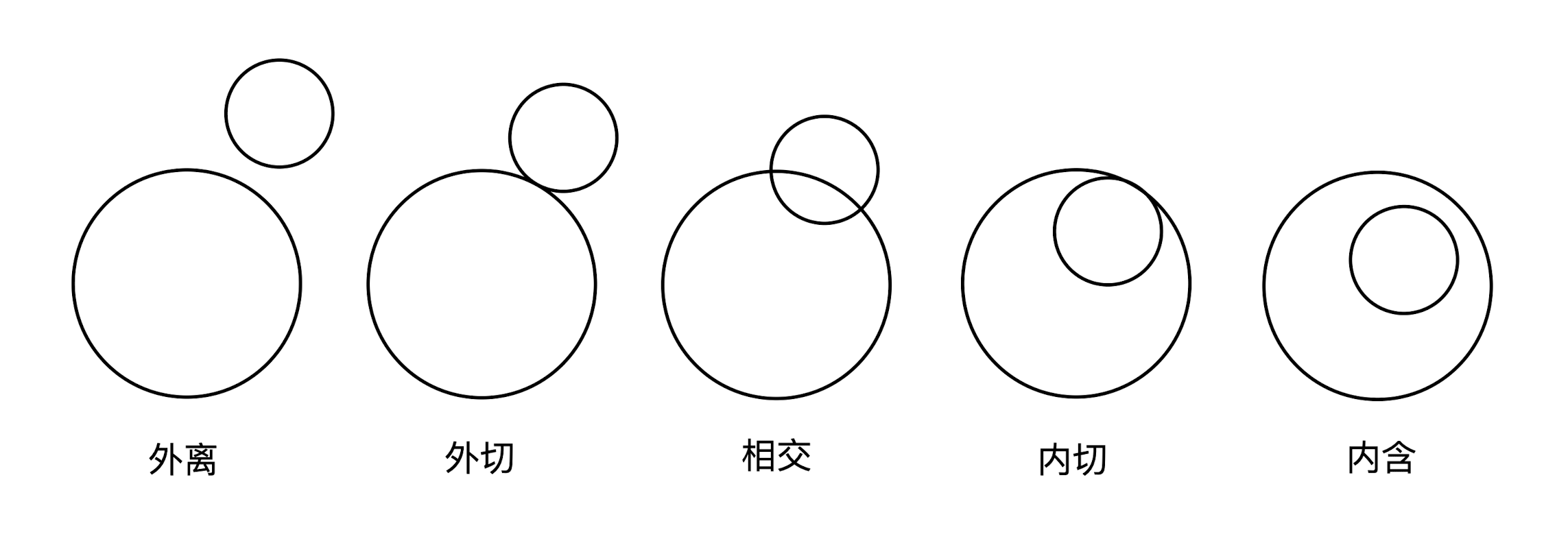
There are five positional relationships between a circle and a circle, as shown in the figure above, where the outer departure and the inner inclusion are collectively called the phase departure, and the outer tangency and the inner tangency are collectively called the phase tangency.

2. Judgment method

Let the circle $C_1 = (x - a) ^ 2 + (y - b) ^ 2 = r ^ 2$ and the circle $C_2 = (x - c) ^ 2 + (y - d) ^ 2 = R^2$, where $r < R$.

  1. Geometric method.

    The relationship between the center distance $d$ and the radius $r,R$ of the two circles is determined.

    • Outward departure: $d > R + r$
    • External tangent: $d = R + r$
    • Intersection: $R - r < d < R + r$
    • Inner cut: $d = R - r$
    • Contains: $d < R - r$

  2. Algebraic method: (obviously this method is more complex)

    The number of solutions to the system of equations can be determined by combining the two circular equations.

    • When $\Delta > 0$, the two circles have $2$ common points and intersect.
    • When $\Delta = 0$, the two circles have $1$ common points, including the inner and outer tangents (tangent).
    • When $\Delta < 0$, the two circles have no common points, including the inner and outer departures (phase departures).

Example.

If the circle $C_1: x^2 + y^2 - 2ax + 4y + a^2 - 5 = 0$, then

Intersect the circle $C_2: x^2+y^2+2 x-2 a y+a^2-3=0$ and find the range of values of $a$.

Solution.

First write it in the form of the standard equation, $C_1:(x-a)^2+(y+2)^2=9,~ C_2:(x+1)^2+(y-a)^2=4$ .

Then the centers and radii of the two circles are $C_1(a,-2), r_1 = 3, and C_2(-1,a), r_2 = 2$ respectively.

Let the distance between the two circles be $d$, then $d^2 = (a + 1) ^ 2 + (- 2 - a) ^ 2 = 2a^2 + 6a + 5$.

Because it is tangent, $3 - 2 < d < 3 + 2 \Rightarrow 1 < d < 5$, then $a \in (-5, -2) \cup (-1,2)$.

XV. The common tangent of two circles

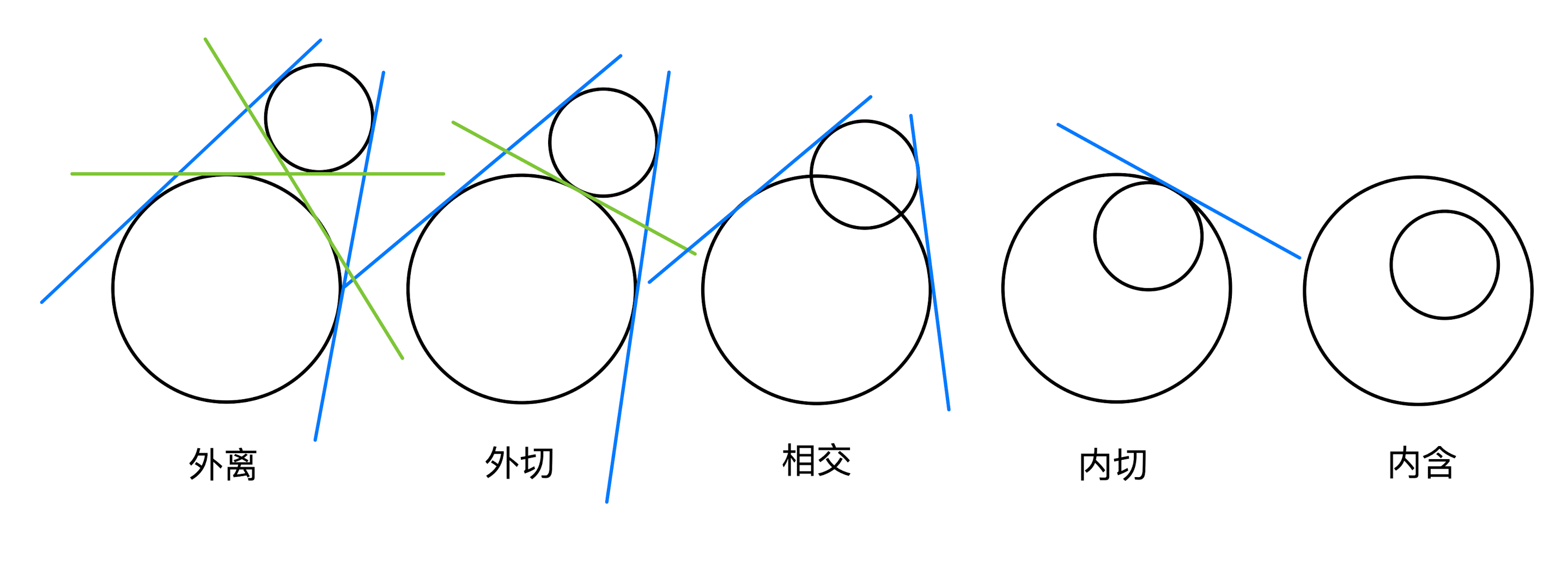
The tangent of two circles is the line tangent to two circles, which can be divided into outer and inner tangents.

  • If two circles are on the same side of a common tangent line, call this common tangent line the outer tangent line of the two circles. (blue)

  • If two circles are on each side of a tangent line, call this tangent line the inner tangent line of the two circles. (green)

As shown above, it can also be organized in the form of the following table. To determine the number of tangents is essentially to determine the relationship between the positions of the two circles.

Memorization method: Subtract from the inner common tangent first, then from the outer common tangent.

Solution of the equation of the common tangent.

When finding the equation of the tangent line of two circles, we must first determine the position of the two circles, so as to determine the number of tangents

Then using the method of coefficients to be determined, let the equation of the common tangent be $y = kx + b$ (note that the special judgment slope does not exist)

Finally, the system of equations for $k,b$ is obtained from the tangency condition, and the values of $k,b$ can be found.

XVI, two circles tangent problem

Properties commonly used when two circles are tangent to each other.

  1. Let the centers of the two circles be $O_1,O_2$ and the radii be $r_1,r_2$, then the two circles are tangent with $\left\{\begin{array}{l}\texttt{internal tangent} \Leftrightarrow\left|O_1 O_2\right|=\left|r_1-r_2\right|\\\texttt{external tangent}
  2. When two circles are tangent, the line connecting the centers of the two circles passes through the tangent point (if the two circles intersect, the line connecting the centers of the two circles bisects the common chord perpendicularly)

Applying these properties in the process of solving problems can sometimes simplify operations considerably.

To deal with the problem of tangency of two circles, we must first accurately grasp whether the tangency is internal or external

If we just tell the two circles are tangent, we must discuss the two cases of tangency and externality.

Second, the problem of tangency of two circles is transformed into “the distance between the centers of two circles” is equal to $|r_1 - r_2|$ or $r_1 + r_2$”.

Example question.

Known circle $C_1: x^2+y^2+2 a x+a^2-4=0~(a \in \mathbb{R})$

with the circle $C_2:x^2 + y^2 - 2by - 1 + b ^ 2 = 0~ ( b \in \mathbb{R})$ having only one common tangent, find $(a + b)_{\min}$.

Solution.

It is easy to know that $C_1(-a,0)$ with radius $r_1 = 2$ and $C_2(0,b)$ with radius $r_2 = 1$.

From the fact that two circles have only one tangent line, we can get two circles are tangent to each other with the distance $|C_1C_2| = \sqrt{a^2 + b^2} = 2 - 1 = 1$, so the two circles are tangent to each other.

So it follows that $a^2 + b^2 = 1$ and let $a = \cos \alpha, b = \sin \alpha~(\alpha \in \mathbb{R})$ , then

$(a+b)_{\min} = -\sqrt{2}$ when and only when $\alpha + \frac{\pi}{4} = -\frac{\pi}{2} + 2k\pi,~k \in \mathbb{Z}$, i.e., $\alpha = -\frac{3}{4}\pi + 2k\pi,~k \in \mathbb{Z}$.

XVII. Two circles common chord problem

1. find the equation of the line where the common chord of two circles lies

Off-topic, the line where this common string is located is called the common cut.

Let the circle $C_1 : x^2+y^2+D_1 x+E_1 y+F_1=0$ and the circle $C_2: x^2+y^2+D_2 x+E_2 y+F_2=0$.

Conclusion: If the circle $C_1$ intersects the circle $C_2$, the equation of the common divisor of the two circles is the subtraction of the equation of the two circles

It should be noted that both circles are in the form of general equations, so don’t subtract the wrong one.

How to understand this equation? We assume that the point $P(x_0,y_0)$ is one of the intersection points.

then $P_0$ must fit the equation of the two circles, and the two equations can be subtracted

Therefore, the point $P$ fits into the original linear equation. The same proof is obtained by doing the same for the other intersection point.

2. the method of finding the common chord length of two circles

  1. Algebraic method.

    Combine the equations of the two circles, solve for the coordinates of the two points of intersection, and use the formula for the distance between the two points to find the common chord length.

  2. Geometric method.

    Find the equation of the line where the common chord is located. Use the right triangle formed by the radius of the circle, the half chord length, and the chord distance to find the chord length by the Pythagorean theorem.

XVIII. The equation of the circle system and its application skills

  1. equation of the concentric circle system.

    Standard equation.

    General equation.

  2. The equation of the system of circles at the same fixed point $(a,b)$ is

  3. The equation of the system of circles at the intersection of the line $Ax + By + C = 0$ and the circle $x^2 + y^2 + Dx + Ey + F = 0$ is

    The equation is understood in the same way as the common cut equation.

  4. The equation of the circle system over the intersection of two circles (both general equations) is

    In particular, this formula is used when two circles are tangent (inner + outer tangent) and $l$ is the equation of the line passing through the common tangent point of the two circles.

Reference.

[1] Apollonios circle - Wikipedia, the free encyclopedia

[2] Summary of knowledge points of tangent equation of a circle _Related videos and test questions online practice_Easy to learn

Author: q779
Link: https://q779.cn/en/en/2022/12/09/the-equation-of-a-circle/
Reprint policy: All articles in this blog are used except for special statements CC BY-NC-ND 4.0 reprint polocy. If reproduced, please indicate source q779 !
Math
评论
  TOC